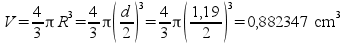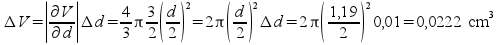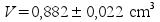Pie de rey
José Antonio Gómez Tejedor
Introducción
El applet simula un pie de rey para la medida de longitudes.Objetivos
- Aprender a utilizar un pie de rey como elemento de medida de longitudes.
Instrucciones
- Sitúa el ratón en el centro de la esfera para poder desplazarla.
-
Mueve la esfera hasta situarla en el píe de rey, de tal forma
que la parte izquierda de la esfera se sitúe junto a la parte
fija del pie de rey.
-
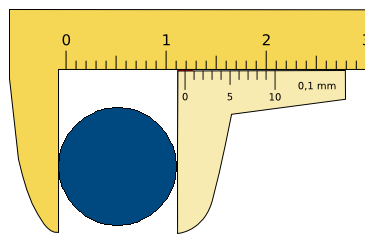
Colocando el ratón en el 0 de la escala inferior, desplaza la
parte móvil del píe de rey hasta situar esta parte
móvil en la parte derecha de la esfera.
-
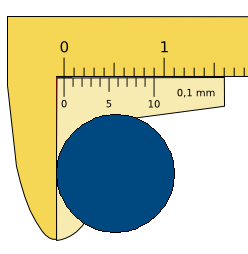
Toma la lectura en la escala del pie de rey:
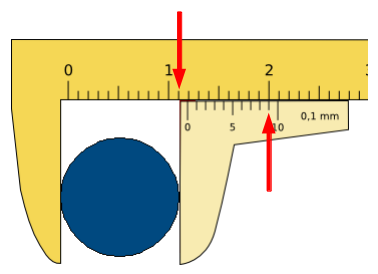
Para ello observa en primer lugar el número que indica la escala superior, más próximo por la izquierda al 0 de la escala inferior: 1,1 cm en el ejemplo de la figura. Después busca las dos líneas que coincidan en la escala inferior y en la superior, y observa el número correspondiente en la escala inferior: 9 en el ejemplo. Esta cifra nos proporciona la siguiente cifra significativa en la medida realizada, de modo que el resultado de la medida es 1,19 cm, con un error de 0,1 mm.
Ejemplo
Mediante el píe de rey se puede medir el diámetro de
varias esferas. De esta forma, se puede diseñar una
práctica de “teoría de errores”, en la cual el alumno, a
partir de la medida del diámetro puede calcular el volumen y
conocida también la masa de la espera, puede medir su densidad,
todo ello con el correspondiente cálculo de errores en medidas
directas e indirectas.
Dicha práctica debe de ir acompañada de una clase
teórica, en la cual se explique todos los conceptos relacionados
con la teoría de errores.
A continuación se muestra un ejemplo en el cual, tras la medida
del diámetro de una esfera, se calcula su volumen con su error
correspondiente.
Siguiendo con el ejemplo de las imágenes mostradas en la parte
superior, el diámetro de la esfera es igual a 1,19 cm.
A partir de ahí, podemos obtener el volumen de la esfera: