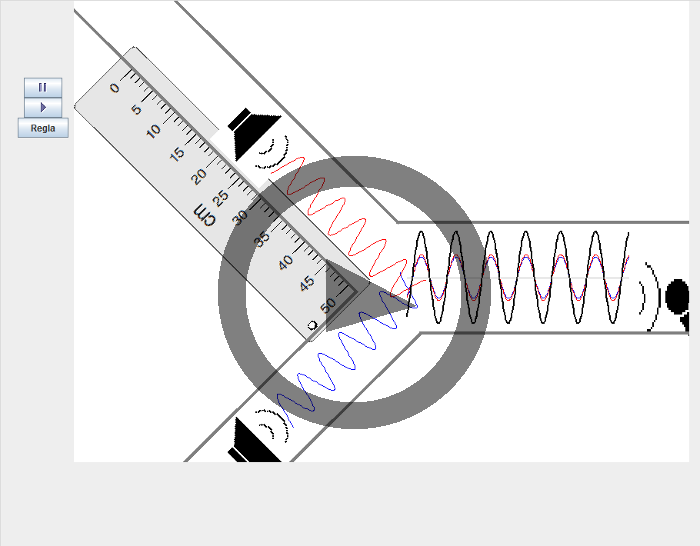
Interferencia de dos ondas
José Antonio Gómez Tejedor
Introducción
El applet simula la emisión de dos ondas sonoras, que interfieren en un punto. Se observan los máximos y mínimos de la interferencia, lo cual permite calcular la velocidad del sonido.Objetivos
- Visualización de la interferencia de dos ondas.
- Cálculo de la velocidad del sonido en el aire.
Instrucciones
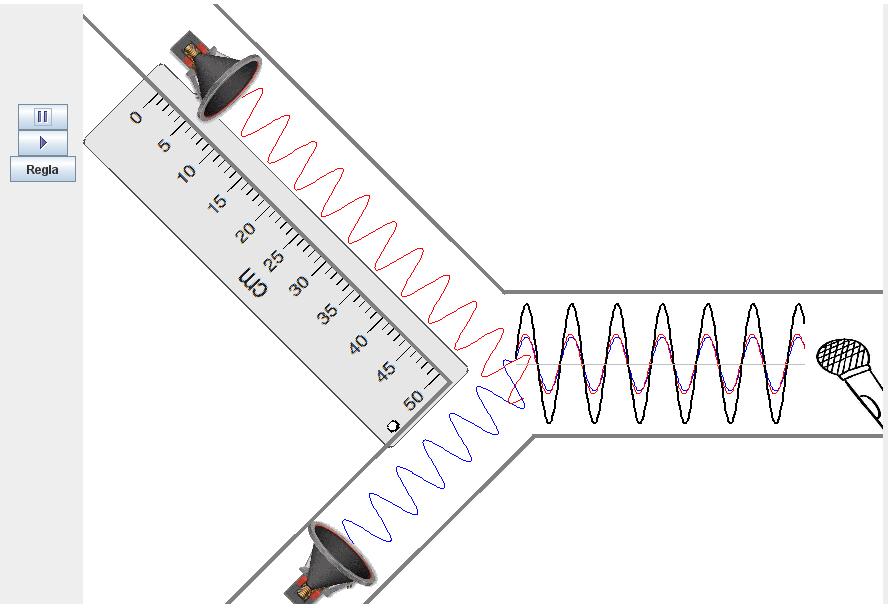
- Mueve sucesivamente el altavoz superior para poder observar en la parte derecha las interferencias constructivas y destructivas de las dos ondas. En azul se muestra la onda del altavoz inferior, y en rojo, la onda del altavoz superior. La superposición de ambas se muestra en color negro.
-
Mediante el botón "Regla"
, puedes hacer
aparecer una regla para medir la posición del altavoz.
Anota la posición de los máximos y mínimos
de interferencia.
-
Utiliza los botones "Play"
/"Pause"
para animar o detener la animación de
las ondas.
Ejemplo
La interferencia de dos ondas armónicas de la misma frecuencia en un punto situado a una distancia r1 del primer foco, y r2 del segundo foco, viene dado por la suma de las dos ondas en dicho punto:
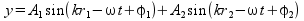
donde A1 y A2 son las amplitudes de las dos ondas, φ1 y φ2 las fases iniciales y ω la frecuencia angular. Si consideramos que las dos fuentes son iguales (misma amplitud y fase inicial que podemos tomar igual a cero para simplificar las expresiones), la amplitud resultante viene dada por
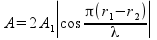
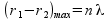
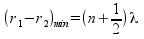
En el ejemplo, dejamos fijo la posición del segundo altavoz r2 (el altavoz situado en la parte inferior), y movemos la posición del primer altavoz (el de la parte superior) r1.
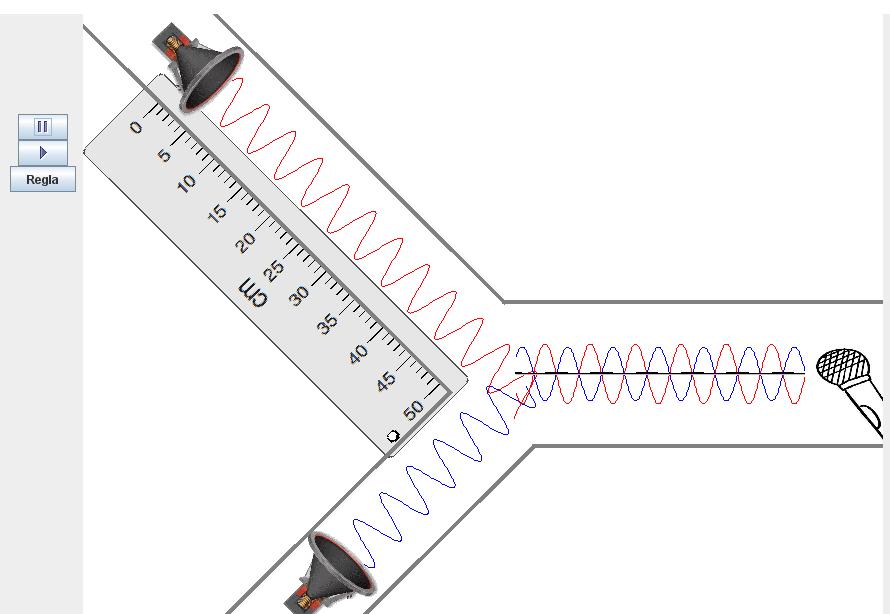
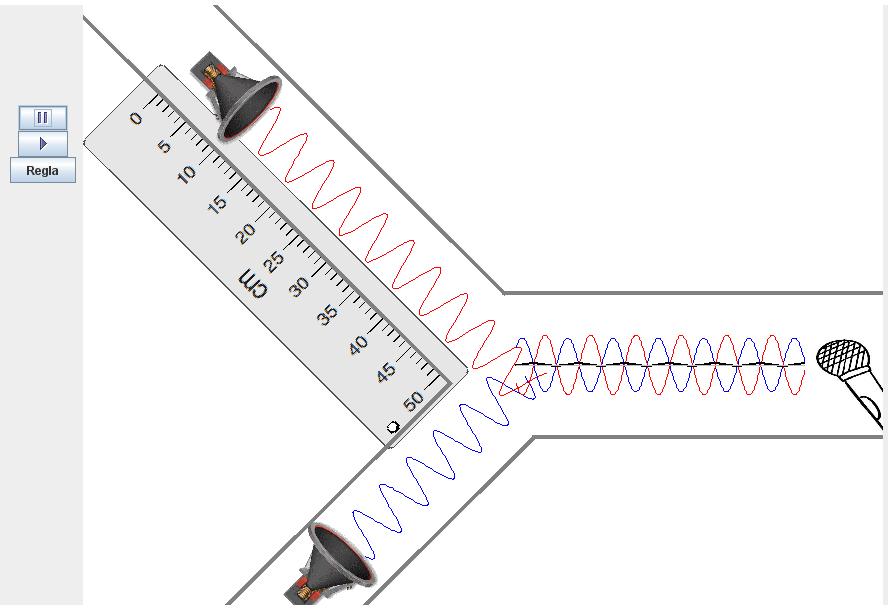
Mediante la regla podemos determinar la posición del primer mínimo en r1=30mm, y la posición del segundo mínimo en r1=100mm, de modo que la diferencia entre ambos mínimos es de 70mm, con lo cual la longitud de onda de la señal es de 70mm. Como la frecuencia de los altavoces se ha fijado en 5kHz, obtenemos que la velocidad del sonido en el aire es igual a v=5·103 × 70·10-3=350m/s.
Applet
