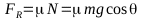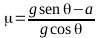Plano inclinado

José Antonio Gómez Tejedor

Introducción

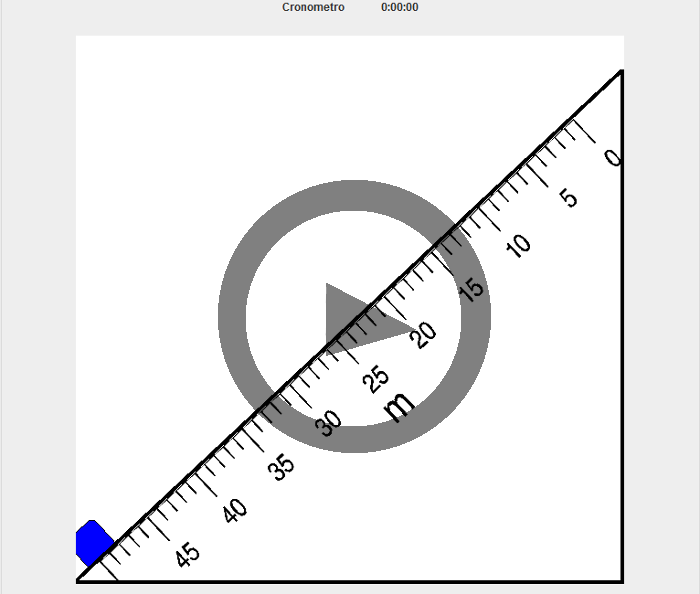
En este applet disponemos de un plano inclinado, sobre el que se deja caer un bloque. A partir del tiempo que tarda el bloque en caer, y la distancia del plano inclinado, podemos determinar la aceleración de caída del bloque. Midiendo el ángulo que forma el bloque con la horizontal podemos determinar también el coeficiente de rozamiento dinámico.

Objetivos

• Estudiar el movimiento de caída de un bloque sobre un plano inclinado.
• Determinar la aceleración de caída del bloque.

Instrucciones

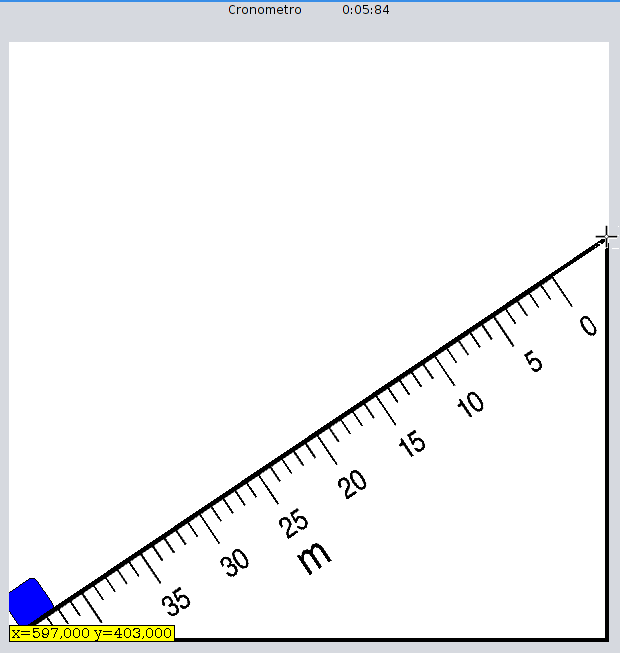
1. Haz clic con el ratón sobre el bloque, y arrástralo hasta la parte superior del plano.
2. Suelta el botón del ratón, y en ese momento el bloque comenzará a deslizar sobre el plano. Al mismo tiempo se pone en marcha el cronómetro.
3. Cuando el bloque llega al final del plano, el cronómetro se detiene, con lo cual obtenemos el tiempo de caída.

Se puede calcular también el ángulo que forma el plano inclinado con la horizontal. Para ello pulsa sobre la esquina superior derecha del plano inclinado, y aparecerán en la parte inferior izquierda, en color amarillo, las coordenadas de dicho punto. A partir de dichas coordenadas podemos obtener el ángulo del plano inclinado.

Ejemplo

En la caída por el plano inclinado el bloque se mueve de acuerdo a un Movimiento Uniformemente Acelerado. De esta forma, la posición del bloque en función del tiempo viene dada por:

En este caso la posición inicial del bloque es x0=0, y además el bloque se suelta con velocidad inicial nula, v0=0, con lo cual tenemos que la distancia recorrida es igual a:

y la aceleración se puede calcular a partir de la distancia recorrida, x, y el tiempo de caída, t:

En el ejemplo de la figura, la distancia que recorre el bloque en el plano inclinado es de 43m, y tarda 5,84s, con lo que la aceleración de caída es:

A partir de las coordenadas de la esquina superior derecha del plano inclinado se puede calcular también el ángulo que forma con la horizontal. En el ejemplo de la figura, dichas coordenadas son x=597 e y=403, con lo cual:

y el valor del coeficiente de rozamiento dinámico es igual a:

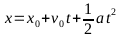
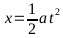
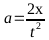
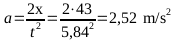
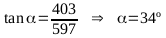
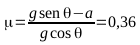
Deducción del coeficiente de rozamiento dinámico

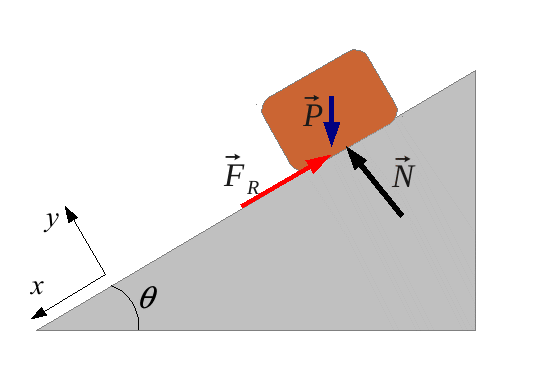
En la figura siguiente se muestra el diagrama de fuerzas de un bloque que desliza sobre un plano inclinado.

A partir de la segunda ley de Newton:

y descomponiendo esta ecuación vectorial en los ejes x e y de la figura:

para el eje x

para el eje y
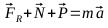
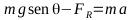
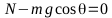
La fuerza de rozamiento viene dada por:

con lo cual podemos obtener el valor del coeficiente de rozamiento dinámico:

Applet