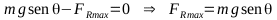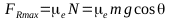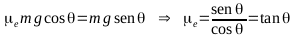Plano inclinado. Determinación del coeficiente de rozamiento estático

José Antonio Gómez Tejedor

Introducción

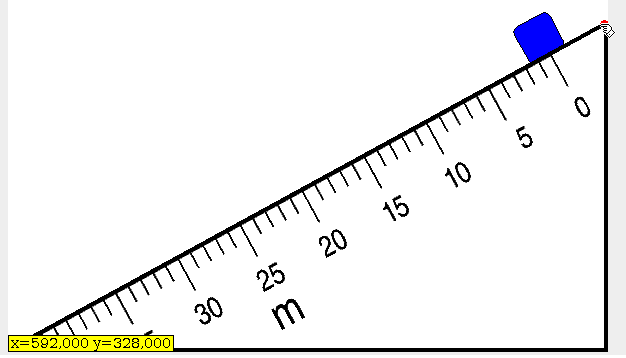
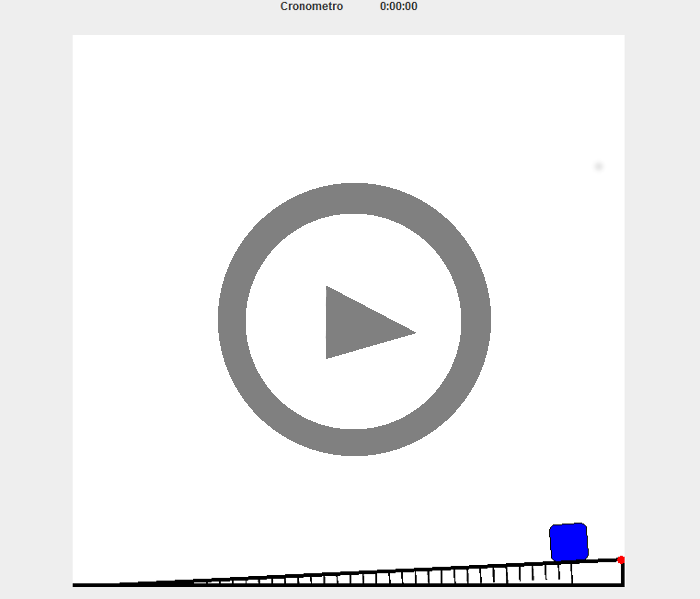
En este applet disponemos de un plano inclinado, en el que se puede variar el ángulo que forma con la horizontal. Sobre dicho plano se encuentra un bloque en reposo. Al ir aumentando el ángulo que forma con la horizontal, en el momento que la componente del peso paralela al plano supera la fuerza de rozamiento estático, el bloque comienza a deslizar por el plano inclinado. A partir de dicho ángulo, podemos determinar el valor del coeficiente de rozamiento estático.

El applet dispone también de un cronómetro para medir el tiempo de caída, y una escala para medir la distancia. Con ello se puede calcular también la aceleración de caída, y el coeficiente de rozamiento dinámico del bloque.

Objetivos

• Estudiar el movimiento de caída de un bloque sobre un plano inclinado.
• Calcular el coeficiente de rozamiento estático.

Instrucciones

1. Pulsa con el ratón sobre el punto rojo situado en la parte superior derecha del plano inclinado.
2. Arrastra el punto hacia arriba lentamente para aumentar el ángulo del plano con la horizontal, hasta que el bloque comience a moverse.
3. En la parte inferior izquierda, en color amarillo, aparecen las coordenadas x e y de dicho punto, con lo cual se puede calcular en ángulo que forma el plano inclinado con la horizontal.

Ejemplo

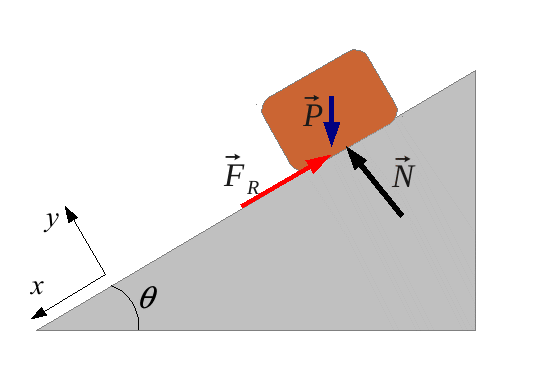
En la figura siguiente se muestra el diagrama de fuerzas de un bloque sobre un plano inclinado.

Donde es la fuerza de rozamiento estático, dado que en este caso estamos analizando el sistema con el bloque en reposo, antes de comenzar el movimiento, siendo la aceleración del sistema nula:

y descomponiendo esta ecuación vectorial en los ejes x e y de la figura:

para el eje x

para el eje y
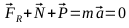
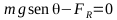
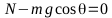
En el momento que el bloque comienza a moverse es cuando la fuerza de rozamiento es igual a la fuerza de rozamiento máximo:

El coeficiente de rozamiento estático se define a partir de dicha fuerza de rozamiento máxima como:

Y de esta forma, igualando ambas expresiones:

Siguiendo el procedimiento descrito anteriormente, en la figura se muestra un ejemplo en el que se ha ido aumentando el ángulo del plano inclinado hasta que el bloque comienza a deslizar.

A partir de las coordenadas del punto superior derecho del plano inclinado (x=592 e y=308) podemos calcular el ángulo, y por tanto el coeficiente de rozamiento estático:

Applet