Física (también “Fundamentos Físicos de la Ingeniería”, “Matemáticas”).

Visualizador del concepto de derivada

Marcos H. Giménez Valentín, Isabel Salinas Marín y Juan Antonio Monsoriu Serra.

*Creado con Easy Java Simulations


Introducción

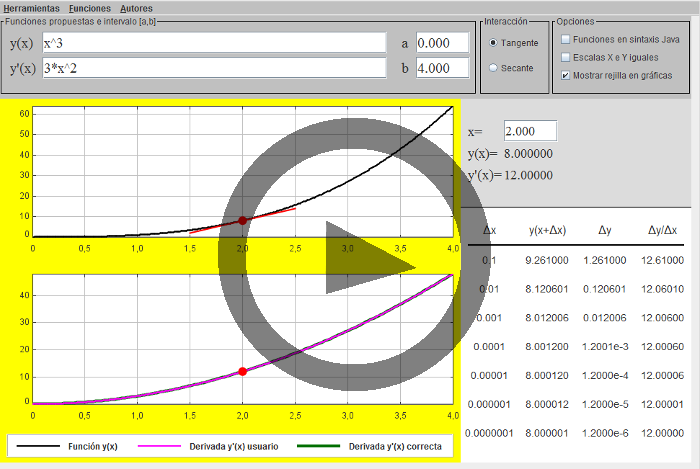
           El applet permite que el usuario introduzca una función escalar de variable escalar, que aparece representada gráficamente en el intervalo deseado. También se muestra gráficamente la derivada de dicha función.
            El usuario puede introducir la que cree que es la derivada de la función. Dicha derivada se muestra gráficamente, y si es correcta coincidirá con la que proporciona el applet.
            El usuario puede seleccionar un valor concreto de la variable independiente x, bien introduciéndolo en un cuadro de texto, bien arrastrando un círculo en el visor que muestra la función. El applet proporciona distinta información para dicho valor, incluyendo el correspondiente valor de la función y el de su derivada.


Objetivos

Instrucciones

  1. Situando el puntero del ratón sobre la mayor parte de los elementos de la interfaz aparece un globo con su descripción.
  2. Al teclear cualquier entrada en un cuadro de texto (los del panel “Funciones propuestas e intervalo [a,b]”, o el etiquetado como “x=” en el panel derecho), dicho cuadro se muestra con fondo amarillo. Es obligatorio pulsar la tecla INTRO para validar la entrada, tras lo que el fondo pasa a ser blanco. Si en lugar de eso el fondo pasa a ser rojo, la expresión o valor introducido no es correcto.
  3. El panel “Funciones propuestas e intervalo [a,b]” permite escribir la expresión de una función y(x), la de su derivada y’(x), y los límites del intervalo [a,b] que se utilizará en la visualización. El formato de las expresiones es en líneas generales el típico de las hojas de cálculo, y con el punto como separador de decimales (p.ej., 3.5*e^(-x)*sin(2*pi*x)). Puede optarse por escribir las funciones en sintaxis Java (p.ej., 3.5*Math.exp(-x)*Math.sin(2*Math.PI*x)) activando la opción “Funciones en sintaxis Java” en el panel “Opciones”.
  4. La gráfica superior muestra la función y(x) en el intervalo indicado. La gráfica inferior muestra en color verde la correspondiente derivada, obtenida numéricamente por el applet, y en color violeta la función y’(x) introducida por el usuario. Si las curvas verde y violeta se superponen, el usuario ha derivado correctamente; si no es así, debe corregir su expresión de la derivada.
  5. Las escalas de las gráficas se seleccionan automáticamente de acuerdo con los rangos en que varían x, y(x) e y’(x), por lo que en general son diferentes entre sí. No obstante, si se quiere considerar que x e y(x) corresponden a la misma magnitud y unidad (como el perfil de una carretera, donde ambas serían longitudes), se puede activar la opción “Escalas X e Y iguales” en el panel “Opciones”. El mismo panel incluye la opción “Mostrar rejilla en gráficas” para activar o desactivar la visualización de la misma.
  6. El menú “Funciones” incluye una biblioteca de funciones estándar. Seleccionando una de ellas, se introducen automáticamente la misma y su derivada en los cuadros de texto y(x) e y’(x), y se asigna un intervalo [a,b] adecuado. Estas funciones sirven también como ejemplo ilustrativo de la sintaxis que se utiliza para escribir las expresiones.
  7. El usuario puede seleccionar un valor de la variable x en el panel de la derecha. A continuación se muestran los correspondientes valores de la función y(x) y de su derivada y’(x) (la dada por el usuario, sea correcta o no). Los correspondientes puntos de las gráficas aparecen marcados mediante sendos círculos rojos. Además, en la gráfica superior se muestra la correspondiente tangente a la curva mediante una línea roja.
  8. En lugar de teclear un valor de la variable x, el usuario puede modificarlo arrastrando cualquiera de los círculos rojos mencionados con el ratón.
  9. Si en el panel “Interacción”, en lugar de la opción “Tangente” se selecciona “Secante”, los círculos rojos pasan a ser azules y ya no son interactivos. A cambio, aparece en la gráfica superior un cuadrado rojo que se puede arrastrar permitiendo elegir un intervalo a la derecha del valor de x seleccionado. El panel derecho muestra ahora los incrementos Δx y Δy en ese intervalo, y la pendiente Δy/Δx del segmento (y por tanto la pendiente media de la curva en ese intervalo).
  10. Arrastrando el cuadrado rojo hacia la izquierda, puede acercarse hasta una distancia horizontal Δx=10-7 del punto azul. El usuario puede observar que la línea secante roja tiende a la tangente, y que la pendiente Δy/Δx tiende a y’(x) (el valor correcto; obviamente, coincidirá con el de la función derivada introducida por el usuario sólo si ésta es correcta). Esta maniobra permite visualizar de forma interactiva el concepto de derivada como un límite.
  11. El panel inferior derecho muestra la misma idea de límite en forma de tabla: para una serie de incrementos de la variable x, cada vez menores, se proporcionan los correspondientes nuevos valores de la función, los incrementos de ésta, y las correspondientes pendientes medias, que convergen hacia el valor de la derivada.
  12. La opción “Reiniciar” en el menú “Herramientas” devuelve el applet a su estado inicial.

Ejemplo

  1. Utilícense la función x3 y el valor x=2 que aparecen seleccionados inicialmente. Si es necesario, púlsese “Reiniciar” en el menú “Herramientas”.
  2. Selecciónese la opción “Secante” en el menú “Interacción”. Desplácese el cuadrado rojo en uno y otro sentido, observando en el panel derecho los incrementos Δx y Δy en el intervalo seleccionado, y la correspondiente pendiente dada por el cociente de ambos, Δy/Δx.
  3. Aproxímese el cuadrado rojo hacia el círculo azul hasta la distancia mínima permitida por el applet. Nótese cómo va variando la pendiente, y cómo se va aproximando al valor 12.
  4. Analícese la tabla del panel inferior derecho. Compruébese que, conforme el incremento de x considerado se hace menor, la pendiente se aproxima al mencionado valor, 12.
  5. Obsérvese que la derivada de y(x)=x3 es y’(x)=3x2, y que y’(2)=12.
  6. Repítase el procedimiento con x=2.5. Compruébese que tanto la tabla como el arrastre del cuadrado rojo indican que el valor límite es 18.75. Compárese este resultado con y’(2.5).
  7. Supóngase que la distancia s recorrida por un móvil en función del tiempo t es s=t3. Hágase el ejercicio mental de cambiar en la interfaz del applet la letra y por s, y x por t. Nótese que Δy/Δx, que sería ahora Δs/Δt, no representaría en este caso una pendiente media, sino una velocidad media. Razónese a partir de todo ello que la función s’(t)=3t2 es la celeridad del móvil. Búsquense otros ejemplos (sugerencia: ¿qué será la derivada de V(t), donde V es el volumen de agua en un depósito en función del tiempo t?).
  8. Introdúzcase en el cuadro de texto y(x) la expresión sin(3*x), y en a y b los valores 0 y 2*pi. Escríbase en el cuadro de texto y’(x) la expresión de la correspondiente derivada. Si es correcta, la línea violeta se superpondrá a la verde.
  9. Una vez introducida la expresión correcta, cos(3*x)*3, y activada la opción “Tangente” en el menú “Interacción”, desplácese con el ratón el círculo rojo de la gráfica superior en uno y otro sentido. Compruébese que la derivada (gráfica inferior) es mayor cuanto más inclinada es la tangente, que es positiva/negativa cuando dicha pendiente es ascendente/descendente, y que es cero en los máximos y mínimos de la función.

Applet