Física (también "Fundamentos Físicos de la Ingeniería", "Electricidad", "Matemáticas").

Visualizador del gradiente y la derivada direccional en un campo escalar bidimensional

Marcos H. Giménez Valentín, Isabel Salinas Marín y Juan A. Monsoriu Serra

Introducción

El applet permite que el usuario seleccione un campo escalar bidimensional entre varios disponibles, apareciendo representado interactivamente en sendas representaciones 2D y 3D. La representación 2D muestra también su gradiente.

El usuario puede arrastrar un círculo y un cuadrado que determinan un punto y una dirección. Un visor muestra la correspondiente sección de la representación 3D, permitiendo visualizar la derivada direccional.

Objetivos

* Visualizar campos escalares bidimensionales y su gradiente.

* Comprobar que la derivada direccional depende tanto del punto como de la dirección.

* Verificar que el gradiente en un punto indica la dirección de la máxima pendiente en ese punto, y que su módulo es el valor de dicha pendiente.

* Comprobar que la derivada direccional en un punto y dirección determinados se obtiene multiplicando escalarmente el gradiente en el punto por el vector unitario de la dirección.

Instrucciones

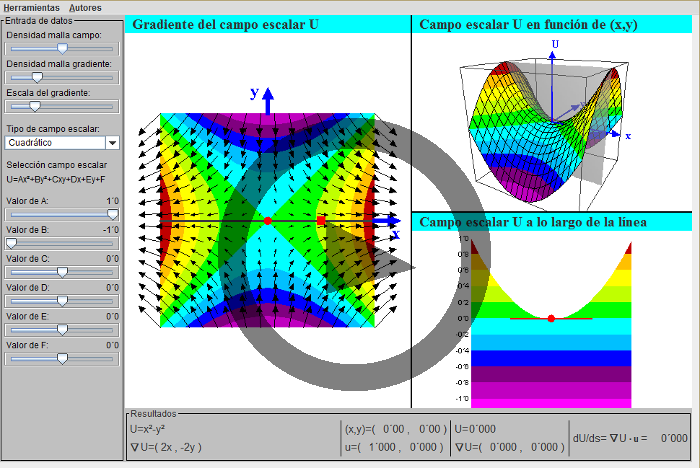
1. La lista desplegable permite elegir un tipo de campo escalar bidimensional U(x,y). Arrastrando las deslizaderas situadas bajo la lista se modifica el valor de los parámetros. Los visores y el panel de resultados se actualizan en tiempo real.

2. El visor principal, "Gradiente del campo escalar U", muestra la función U(x,y) como un plano topográfico, con los distintos colores representando intervalos de 0'2 unidades (excepto los extremos, que indican valores menores de -1 y mayores de +1). El intervalo que corresponde a cada color puede verse en el visor "Campo escalar U a lo largo de la línea").

3. En el visor principal se muestra una línea gris, junto con un círculo y un cuadrado rojos que operan como asas. Es posible desplazar el círculo para seleccionar un punto, y el cuadrado para elegir una dirección. Al hacerlo, los visores de la derecha y el panel de resultados se actualizan en tiempo real.

4. El visor principal muestra también, mediante flechas, el gradiente del campo U en los puntos de una malla rectangular. La densidad de esa malla se puede modificar arrastrando la deslizadera de título "Densidad malla gradiente". Para facilitar la visualización, puede variarse la escala de las flechas arrastrando la deslizadera de título "Escala del gradiente".

5. El visor superior derecho, "Campo escalar U en función de (x,y)", representa verticalmente el campo escalar bidimensional. También aparece un plano que indica la sección seleccionada mediante la línea gris del visor principal. La esfera roja corresponde al círculo rojo del visor principal. Arrastrando con el ratón se puede modificar el punto de vista. Se puede recuperar la perspectiva inicial pulsando sobre la opción "Restaurar vista" en el menú "Herramientas".

6. El visor inferior derecho, "Campo escalar U a lo largo de la línea", representa verticalmente el campo escalar bidimensional en los puntos de la línea gris del visor principal. Equivale a la sección según el plano que se muestra en el visor superior derecho. El punto que aparece se corresponde con la posición del círculo de la línea gris, y la línea recta muestra la línea tangente, cuya pendiente es la derivada direccional.

7. La deslizadera de título "Densidad malla campo" controla la densidad de la malla para la representación del campo escalar en los visores. Aumentando esta densidad se mejora la calidad de la visualización, pero también se ralentiza la respuesta a las acciones del usuario.

8. El panel de resultados muestra: la expresión del campo escalar y la de su gradiente; las coordenadas del punto y el vector unitario de la dirección, seleccionados mediante las asas de la línea gris del visor principal; los valores del campo y del gradiente en el punto escogido; y el de la derivada direccional. Situando el ratón sobre cualquiera de los textos aparece un globo con su descripción.

9. La opción "Reiniciar" en el menú "Herramientas" devuelve la simulación a su estado inicial.

Ejemplo

1. Utilícese el campo escalar U = x ² -y ² que aparece seleccionado inicialmente.

2. Desplácese el cuadrado rojo en el visor principal. Obsérvese cómo varía la sección dependiendo de la dirección del corte. Nótese que cuando la línea gris forma un ángulo de 45º la sección es una línea horizontal, y que a partir de ahí el mínimo pasa a ser un máximo.

3. Desplácese el círculo rojo del visor principal a la posición (0'5,0'5), y el cuadrado hasta que el vector unitario de la dirección sea (1,0) (tanto las coordenadas como el vector se muestran en el panel de resultados). Compruébese que en ese punto el campo U = x ² -y ² es 0, y su gradiente
∇U = (2x, 2y) vale (1, 1). Compruébese también que la derivada direccional es 1.
4. Desplácese el cuadrado rojo del visor principal comprobando cómo varía la derivada direccional. Obsérvese que cuando la sección tiene la dirección del gradiente, 45º por debajo del eje X, se obtiene la mayor derivada direccional para el punto considerado. Véase también que, en efecto, en esa dirección se muestra la tangente con mayor pendiente en el visor inferior derecho.

Applet