Física (también “Fundamentos Físicos de la Ingeniería”, “Mecánica”)
Visualizador del concepto de integral definida.
Marcos H. Giménez Valentín, Isabel Salinas Marín y Juan Antonio Monsoriu Serra
*Creado con Easy Java Simulations
Introducción
El applet permite que el usuario introduzca una función escalar de variable escalar, que aparece representada gráficamente en el intervalo deseado, y que seleccione un intervalo de integración.El usuario puede optar entre diferentes números de subdivisiones del intervalo de integración. La gráfica muestra la correspondiente división en rectángulos de la superficie delimitada por el eje x, la curva y los extremos del intervalo. Una tabla muestra las áreas de todos o parte, según su número, de esos rectángulos, y la suma total. También se muestra esa suma para los diferentes números de subdivisiones contemplados. Esto permite visualizar el concepto de integral definida como un límite.
El usuario puede introducir la que cree que es la primitiva de la función. El applet proporciona la resta de los valores de la primitiva para los límites del intervalo de integración (esto es, la integral definida), y si es correcta coincidirá aproximadamente con el área calculada con 2000 rectángulos, que es el número máximo contemplado por el programa por motivos de velocidad de respuesta.
Objetivos
- Visualizar gráficamente cómo se puede obtener el área delimitada por una función en un intervalo mediante un número creciente de rectángulos cada vez más delgados.
- Entender el concepto de integral definida como un límite.
- Comprobar que se sabe integrar.
Instrucciones
- Situando el puntero del ratón sobre la mayor parte de los elementos de la interfaz aparece un globo con su descripción.
- Al teclear cualquier entrada en un cuadro de texto (los del panel “Funciones propuestas e intervalo [a,b]”, o los etiquetados como “x1=” y “x2=” en el panel derecho), dicho cuadro se muestra con fondo amarillo. Es obligatorio pulsar la tecla INTRO para validar la entrada, tras lo que el fondo pasa a ser blanco. Si en lugar de eso el fondo pasa a ser rojo, la expresión o valor introducido no es correcto.
- El panel “Funciones propuestas e intervalo [a,b]” permite escribir la expresión de una función y(x), la de su primitiva Y(x), y los límites del intervalo [a,b] que se utilizará en la visualización. El formato de las expresiones es en líneas generales el típico de las hojas de cálculo, y con el punto como separador de decimales (p.ej., 3.5*e^(-x)*sin(2*pi*x)). Puede optarse por escribir las funciones en sintaxis Java (p.ej., 3.5*Math.exp(-x)*Math.sin(2*Math.PI*x)) activando la opción “Funciones en sintaxis Java” en el panel “Opciones”.
- El usuario puede seleccionar los límites inferior x1 y superior x2 del intervalo de integración en el panel de la derecha. También puede optar entre diferentes números de subdivisiones del intervalo de integración. La gráfica muestra la correspondiente división en rectángulos de la superficie delimitada por el eje x, la curva dada por y(x), y los extremos x1 y x2 del intervalo. Una tabla muestra las áreas de todos o parte, según su número, de esos rectángulos, y la suma total. También se muestra esa suma para los diferentes números de subdivisiones contemplados. Esto permite observar que se puede obtener el área delimitada por una función en un intervalo mediante un número creciente de rectángulos cada vez más delgados.
- El panel derecho muestra la resta de los valores de la primitiva Y(x) (la dada por el usuario, sea correcta o no). Si dicha resta coincide aproximadamente con el área calculada con 2000 rectángulos, y lo hace para cualquier intervalo de integración [x1,x2], el usuario ha integrado correctamente; si no es así, debe corregir su expresión de la primitiva.
- El intervalo [a,b] que se muestra en la gráfica ha de contener al intervalo de integración [x1,x2]. Si el usuario introduce algún valor incompatible con este requisito, el applet realiza los ajustes pertinentes.
- Activando la opción “Sincronizar los intervalos [a,b] y [x1,x2]” en el panel “Opciones”, éstos serán automáticamente idénticos, de modo que el tramo visualizado en la gráfica se corresponderá con el intervalo de integración.
- Las escalas de la gráfica se seleccionan automáticamente de acuerdo con los rangos en que varían x e y(x), por lo que en general son diferentes entre sí. No obstante, si se quiere considerar que x e y(x) corresponden a la misma magnitud y unidad, se puede activar la opción “Escalas X e Y iguales” en el panel “Opciones”. El mismo panel incluye la opción “Mostrar rejilla en gráfica” para activar o desactivar la visualización de la misma.
- El menú “Funciones” incluye una biblioteca de funciones estándar. Seleccionando una de ellas, se introducen automáticamente la misma y su primitiva en los cuadros de texto y(x) e Y(x), y se asignan unos intervalos [a,b] y [x1,x2] adecuados. Estas funciones sirven también como ejemplo ilustrativo de la sintaxis que se utiliza para escribir las expresiones.
- La opción “Reiniciar” en el menú “Herramientas” devuelve el applet a su estado inicial.
Ejemplo
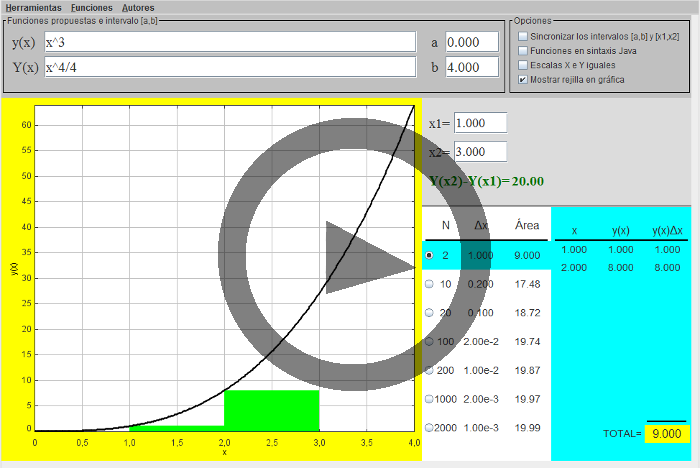
- Utilícense la función x3 y el intervalo de integración [1,3] que aparecen seleccionados inicialmente. Si es necesario, púlsese “Reiniciar” en el menú “Herramientas”.
- Obsérvese que la gráfica muestra el intervalo de integración subdividido en dos tramos, [1,2] y [2,3]. Cada uno de ellos constituye la base de un rectángulo cuya altura es el valor inicial de la función, y(1)=13=1 para el primero e y(2)=23=8 para el segundo.
- Nótese que las áreas de dichos rectángulos son 1×1=1 para el primero, y 1×8=8 para el segundo, siendo 9 la correspondiente suma. Estos valores aparecen reflejados en la tabla de fondo azul, en el panel derecho.
- Selecciónese N=10 en el panel derecho. Obsérvese en la gráfica la nueva subdivisión en 10 intervalos, y los correspondientes 10 rectángulos. La tabla de fondo azul muestra ahora los valores de sus alturas, sus áreas, y el área total.
- Selecciónense sucesivamente valores crecientes de N, hasta llegar a 2000. Nótese que el área total del creciente número de rectángulos se aproxima cada vez más a la de la superficie delimitada por la función y el eje x en el intervalo [x1,x2]. Obsérvese que el valor al que se aproxima es 20.
- La primitiva de y(x)=x3 es Y(x)=x4/4. Obsérvese que la integral definida de x3 en el intervalo [1,3] es Y(3)-Y(1)=34/4-14/4=20.
- Repítase el procedimiento con el intervalo de integración [1.5,4]. Compruébese que, de acuerdo con la tabla, el valor límite del área total de un número creciente de rectángulos cada vez más delgados debe ser próximo a 62.70. Compárese este resultado con Y(4)-Y(1.5).
- Supóngase que la velocidad v de un móvil en función del tiempo es v=t3. Hágase el ejercicio mental de cambiar en la interfaz del applet la letra y por v, y x por t. Nótese que el área de un rectángulo cualquiera, yΔx, que sería ahora vΔt, representaría en este caso el espacio recorrido suponiendo que v no varía en ese Δt. Razónese a partir de todo ello que la integral definida es el espacio recorrido por el móvil. Búsquense otros ejemplos (sugerencia: ¿qué será la integral definida en el intervalo [t1,t2] de Q(t), donde Q es el caudal de agua que entra en un depósito en función del tiempo t?).
- Introdúzcase en el cuadro de texto y(x) la expresión sin(x), y en x1 y x2 los valores 0 y pi. Escríbase en el cuadro de texto Y(x) la expresión de la correspondiente primitiva. Si es correcta, el valor de Y(x2)-Y(x1) mostrado en el panel derecho coincidirá aproximadamente con el área total de 2000 rectángulos.
- Una vez comprobada la expresión correcta de Y(x), -cos(x), cámbiese el valor de x2 por 1.5*pi. Compruébese que el área delimitada por la curva es ahora menor que antes. Nótese que esto se debe a que las áreas por debajo del eje x son negativas, ya que en el intervalo [π,1.5π] es y<0, y por tanto yΔx<0, esto es, el área de los correspondientes rectángulos es también negativa.
- Cámbiese el valor de x1 por pi. Obsérvese el signo de la correspondiente área. Búsquese y justifíquese la relación existente entre las áreas (y por tanto las integrales definidas) en los tres intervalos analizados, [0,π], [π,1.5π] y [0,1.5π].