Ondas estacionarias

Tubo de Rubens

José Antonio Gómez Tejedor

Introducción:

El Tubo de Rubens es un dispositivo que permite la visualización de ondas sonoras. Consiste en un tubo, que se llena de gas inflamable. En uno de los extremos del tubo se coloca un altavoz, y el otro permanece cerrado. Sobre el tubo se realizan una serie de pequeños orificios que permiten la salida del gas, prendiendo el gas a su salida por los orificios. En las zonas donde la amplitud de la onda sonora es mayor, la presión aumenta, y eso produce que la llama en ese punto sea más alta, y por el contrario donde la presióes menor la llama es más baja, o incluso desaparece cuando la presión externa es mayor que la presión en el interior del tubo, impidiendo la salida del gas por esos puntos. De esta forma, podemos visualizar de manera muy espectacular y llamativa las ondas sonoras que se propagan en el interior del tubo.

El altavoz se conecta a un generador de funciones, que proporciona una señal sinusoidal, de modo que dentro del tubo tenemos la propagación de dicha onda sonora, junto con las ondas reflejadas en el extremo del tubo.

A partir de la medida de la distancia entre nodos en la onda, y conocida la frecuencia del generador, podemos determinar de forma sencilla la velocidad del sonido en el tubo.

Una de las características fundamentales del tubo de Rubens es su espectacularidad. Con esta simulación no se pretende sustituir dicho dispositivo, sino que intenta ser una ayuda para el profesor a la hora de introducir su funcionamiento. Permite que el profesor explique como se realizan las medidas sobre el tubo de Rubens, y permite que los alumnos entiendan mejor su funcionamiento.

Objetivos:

Analizar la propagación de ondas estacionarias en un tubo.
Calcular la velocidad del sonido en el aire.

Instrucciones:

En la parte superior, la aplicación dispone de:

Dos botones, para el encendido y apagado del generador de funciones.
A continuación dispone de una barra deslizante para regular la amplitud de la señal.
Otra barra deslizante para ajustar la frecuencia del generador.
Por último, dispone de dos botones para el ajuste fino de la frecuencia, que permite variar la frecuencia del generador a intervalos de 0,5 Hz.

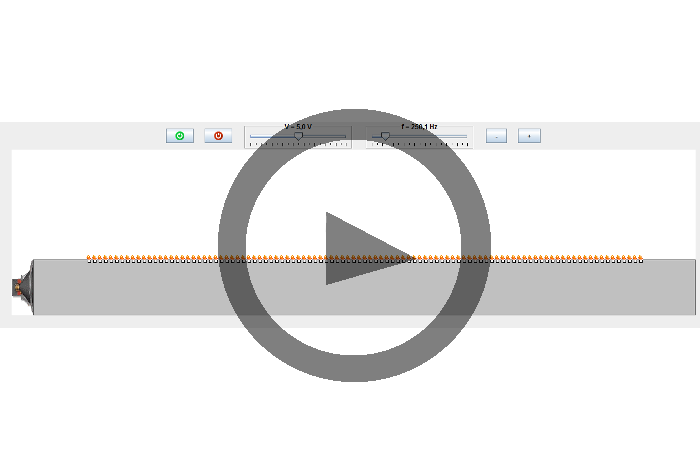
En la parte inferior se encuentra la animación en sí, donde aparece el tubo, y las llamas, cuya altura depende de la amplitud de la señal dentro del tubo. En los puntos donde la presión dentro del tubo es inferior a la presión externa, el gas no puede salir por los orificios y no existe llama. Cuanto más grande es la presión en el interior del tubo, mayor altura alcanzan las llamas.

Ejemplo

A continuación se muestra un par de ejemplos de la medida de la velocidad del sonido en el interior del tubo. Para ello, en primer lugar el alumno debe de seleccionar una frecuencia de resonancia del tubo, para conseguir una onda estacionaria. En dicha situación, la separación entre dos nodos consecutivos es igual a la mitad de la longitud de onda de la señal que se propaga en el interior del tubo. Midiendo dicha distancia, y conociendo la frecuencia del generador, el alumno puede determinar la velocidad del sonido en el interior del tubo: v= λ f .

Para medir dicha distancia, disponemos de la información adicional de que la separación entre dos agujeros consecutivos del tubo, en este caso, es igual a 1cm. También se puede utilizar el cursor del ratón para medir distancias: pulsando sobre cualquier punto de la pantalla, en la esquina inferior izquierda, resaltado en amarillo aparecen las coordenadas (x,y) del puntero del ratón. De esta forma, se puede medir la distancia de separación entre dos puntos cualquiera de la pantalla. Dichas coordenadas vienen dadas en mm.

En este primer ejemplo, la separación entre los dos nodos consecutivos es de 841 - 435 = 406 mm, de modo que la longitud de onda y la velocidad del sonido son respectivamente:

λ = 2 • 0,406 = 0,812 m

= λ f = 0,812 • 431,2 = 350,1 m/s

En este segundo ejemplo, la separación entre los dos nodos consecutivos es de 558 – 378 = 180 mm, de modo que la longitud de onda y la velocidad del sonido son respectivamente:

λ = 2 • 0,180 = 0,360 m

v= λ f = 0,360 • 1006,2 = 362,2 m/s

Las diferencias en los valores observados en ambos ejemplos son debidas a los errores experimentales a la hora de medir las distancias sobre el tubo de Rubens, y a la hora de encontrar las frecuencias de resonancia de forma precisa. Dichas dificultades experimentales son las mismas que las que puede encontrar un alumno en el desarrollo de las medidas en un dispositivo real.