Óptica geométrica
Diagrama de rayos para una lente divergente delgada
José Antonio Gómez Tejedor
Introducción
Este applet permite visualizar el diagrama de rayos de una lente divergente para la formación de la imagen. Además, el alumno puede realizar diversas medidas sobre la pantalla del ordenador: distancias focales, posición del objeto y de la imagen, tamaño del objeto y la imagen.La aplicación permite además variar la posición y tamaño del objeto, así como la distancia focal de la lente.
Objetivos
Aprender a trazar el diagrama de rayos de una lente divergente.
Aprender a calcular el tamaño y posición de la imagen en una lente divergente.
Instrucciones:
Al comenzar la aplicación, podemos ver una lente divergente, cuya distancia focal tiene un valor inicial aleatorio. Se puede observar también un objeto, así como la imagen formada por la lente de dicho objeto. Además se observa el diagrama de rayos correspondiente, donde se puede observar el rayo que pasa por el primer punto focal que se desvía hacia el infinito (paralelo al eje óptico), el rayo central, que no sufre ningunas desviación, y el rayo proveniente del infinito (paralelo al eje óptico) que pasa por el segundo punto focal de la lente. El primer y segundo punto focal de la lente aparecen indicado sobre el eje óptico mediante un punto rojo y uno azul respectivamente, y pueden cambiarse, simplemente pulsando con el puntero del ratón, y arrastrando a izquierda y derecha.
El tamaño y posición del objeto también puede variarse de forma arbitraria, de la misma forma.
Conocida la posición del objeto, s, y la distancia focal de la lente, f, podemos calcular la posición de la imagen, s', mediante la ecuación:
Y el tamaño de la imagen viene dada por,
Ejemplo
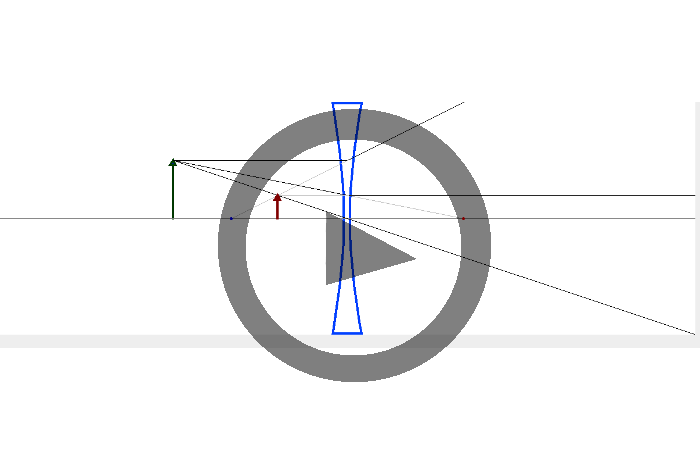
En la figura se muestra un ejemplo de la imagen formada por la lente divergente de un objeto. Para medir cualquier distancia en la pantalla del ordenador, basta con pulsar sobre cualquier punto de la pantalla, y en la parte inferior izquierda aparece en color amarillo las coordenadas del punto en cuestión. Midiendo la posición de dos puntos, se puede calcular la distancia entre ambos puntos. Las distancias vienen dadas en mm.
En ese ejemplo, a partir de las medidas realizadas en la pantalla se obtiene f = –200 mm, s = 300 mm, y y=100 mm. En la figura, se muestra a modo de ejemplo, las determinación de las coordenadas de uno de los puntos de la imagen (x=480 mm y y=244 mm). Del mismo modo, a partir de la medida de las coordenadas del resto de puntos, se obtienen todos los parámetros necesarios.
A partir de estos datos podemos calcular la posición de la imagen:
Y el tamaño de la imagen viene dada por,
Por otro, midiendo directamente sobre la pantalla del ordenador se obtiene s' = – 119 mm y y'= 41 mm (imagen virtual derecha). Vemos que hay unas pequeñas diferencias entre el valor obtenido en la medida directa sobre la pantalla, y en el resultado calculado. Esto es debido a los errores cometidos en la toma de datos sobre la pantalla del ordenador, de la misma forma que ocurriría en el laboratorio en un experimento real.
El alumno deberá realizar tres medidas de cada magnitud, y calcular valores medios y desviación típica, de la misma manera que en una experiencia real en le laboratorio de física.