Transmisión de calor en estado transitorio. Excitación senoidal

• Emilio J. Sarabia Escriva [emsaes@upvnet.upv.es]

• Víctor Soto Francés [vsoto@ter.upv.es]

• Jose Manuel Pinazo Ojer [jmpinazo@ter.upv.es]

Dpto. Termodinámica Aplicada

Introducción

El presente laboratorio virtual muestra el comportamiento en régimen transitorio de una placa plana en función de sus propiedades térmicas. Se representa la evolución de temperatura y flujo de calor en el interior del material cuando se aplica una excitación de temperaturas senoidal en una de las superficies, manteniendo la otra superficie a temperatura constante.

Objetivos

• Mostrar la evolución de temperaturas en el interior de una pieza plana con excitación senoidal de temperaturas en una se sus superficies.

• Observar la influencia de las propiedades del material en el problema.

Instrucciones

• Definir las propiedades físicas del material y el valor de la excitación de temperaturas.

• Definir el punto x[m] interior de la pieza que se desea analizar para ser representado en la gráfica.

• La gráfica se refresca al salir de las casillas donde se editan los valores.

Descripción del problema

El proceso representa la evolución de la temperatura y el flujo de calor en el interior de una pieza homogénea en forma de placa plana. Se considera que la superficie x=espesor[m] tiene una excitación senoidal de temperaturas. La superficie correspondiente a x=0[m] se considera que se mantiene a una temperatura constante igual a la media de la evolución senoidal.

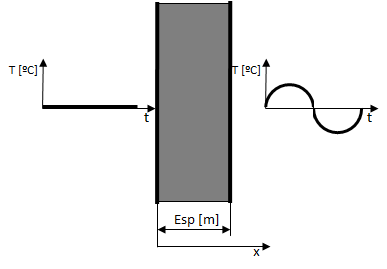
Se define la evolución de temperaturas en x=espesor[m] como:

$$T(x=esp,t)=Amplitud·sin(w·t+desfase)=Im(Amplitud·e^{i(w·t+desfase)})$$

La temperatura para x=0[m] la consideramos constante:

$$T(x=0,t)=0$$

La función que representa la temperatura en el interior de la pieza (x [m]) para un tiempo (t [s]) viene de la expresión:

$$T(x,t)=Im(Amplitud·{sinh(M·x·(1+i))}/{sinh(M·L·(1+i))}·e^(i(w·t+desfase)))$$ Siendo:

• $M=√{{w}/{2α}} [1/m]$

• Siendo la frecuencia: $w={2π}/{periodo[h]·3600} [Hz]$

• Siendo la difusividad: $α={k}/{densidad·Cp} [m^2/s]$

El flujo de calor en el interior de la pieza (x [m]) para un tiempo (t [s]) se describe con la expresión:

$$q(x,t)=Im(-Conductividad·Amplitud·M·(1+i)·{cosh(M·x·(1+i))}/{sinh(M·L·(1+i))}·e^{i(w·t+desfase)})$$

Propiedades térmicas del material:

Densidad [kg/m3]	Cp [J/(kg·K)]	Conductividad [W/(m·K)]	Espesor [m]
1000	1000	1	0.6

Propiedades de la excitación senoidal:

Amplitud de la señal[ºC]	Periodo de la señal [h]
10	24

Punto de análisis:

x [m]
0.3

Representación gráfica